RC Charging Circuit

All Electrical or Electronic circuits or systems suffer from some sort of “time-delay” between its input and output, once a proof or voltage, either continuous, ( DC ) or alternating ( AC ) is foremost applied to that.
            This delay is generally called the time delay or Time Constant of the circuit and it's the time response of the circuit once a step voltage or signal is foremost applied. The resultant time constant of any electronic circuit or system can chiefly rely upon the reactive parts either electrical phenomenon or inductive connected to that and could be a measure of the time interval with units of, Tau – τ

When AN increasing DC voltage is applied to a discharged capacitance, the capacitance attracts a charging current and “charges up”, and once the voltage is reduced, the capacitance discharges within the other way. as a result of capacitors area unit able to store power they act like little batteries and might store or unharness the energy as needed.

The charge on the plates of the capacitance is given as: letter of the alphabet = CV. This charging (storage) and discharging (release) of a capacitances energy is rarely instant however takes a precise quantity of your time to occur with the time taken for the capacitor to charge or discharge to among a precise share of its most offer worth being referred to as its Time Constant ( τ ).

If a resistance is connected nonparallel with the capacitance forming AN RC circuit, the capacitance can upset bit by bit through the resistance till the voltage across the capacitance reaches that of the provision voltage. The time additionally known as the transient response, needed for the capacitance to completely charge is corresponding to concerning five time constants or 5T.

This transient time interval T, is measured in terms of τ = R x C, in seconds, wherever R is that the worth of the resistance in ohms and C is that the worth of the capacitance in Farads. This then forms the premise of AN RC charging circuit were 5T can even be thought of as “5 x RC”.

RC Charging Circuit

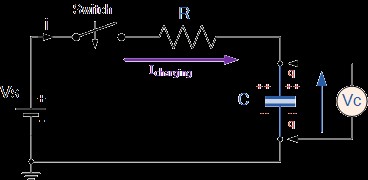
The figure below shows a capacitance, ( C ) nonparallel with a resistance, ( R ) forming a RC Charging Circuit connected across a DC battery offer ( Vs ) via a mechanical switch. once the switch is closed, the capacitance can bit by bit upset through the resistance till the voltage across it reaches the provision voltage of the battery. the style within which the capacitance charges up is additionally shown below.
Let us assume higher than, that the capacitance, C is absolutely “discharged” and therefore the switch (S) is absolutely open. These area unit the initial conditions of the circuit, then t = 0, i = zero and letter of the alphabet = zero. once the switch is closed the time begins at t = zero and current begins to flow into the capacitance via the resistance.

Since the initial voltage across the capacitance is zero, ( Vc = zero ) the capacitance seems to be a brief circuit to the external circuit and therefore the most current flows through the circuit restricted solely by the resistance R. Then by exploitation Kirchhoff’s voltage law (KVL), the voltage drops round the circuit area unit given as:

kirchoffs voltage law

The capacitance currently starts to upset as shown, with the increase within the RC charging curve vessel at the start as a result of the charging rate is quickest at the beginning and so tapers off because the capacitance takes on extra charge at a slower rate.

As the capacitance charges up, the potential drop across its plates slowly will increase with the particular time taken for the charge on the capacitance to achieve sixty three of its most potential voltage, in our curve zero.63Vs being referred to as just the once Constant, ( T ).

This 0.63Vs voltage purpose is given the abbreviation of 1T, (one time constant).

The capacitance continues charging up and therefore the voltage distinction between Vs and Vc reduces, therefore to will the circuit current, i. Then at its final condition bigger than 5 time constants ( 5T ) once the capacitance is alleged to be absolutely charged, t = ∞, i = 0, q = Q = CV. Then at time this diminishes to zero, the capacitance acts like AN electrical circuit condition thus, the dip is entirely across the capacitance.

So mathematically we will say that the time needed for a capacitance to upset to at least one time constant, ( 1T ) is given as:

RC Time Constant, TauThis RC time constant solely specifies a rate of charge wherever, R is in Ω‘s and C in Farads.

Since voltage V is expounded to charge on a capacitance given by the equation, Vc = Q/C, the voltage across the worth of the voltage across the capacitance ( Vc ) at any instant in time throughout the charging amount is given as:

RC Charging Circuit Example No1

Calculate the RC time constant, τ of the subsequent circuit.

rc charging circuit exampleThe time constant, τ is found exploitation the formula T = R x C in seconds.
Therefore the time constant τ is given as: T = R x C = forty sevenk x 1000uF = 47 Secs

a) What worth are going to be the voltage across the capacitance at zero.7 time constants?

At 0.7 time constants ( zero.7T ) Vc = zero.5Vs. Therefore, Vc = 0.5 x 5V = 2.5V

b) What worth are going to be the voltage across the capacitance at one time constant?

At one time constant ( 1T ) Vc = zero.63Vs. Therefore, Vc = 0.63 x 5V = three.15V

c) however long can it desire “fully charge” the capacitor?

The capacitance are going to be absolutely charged at five time constants.

1 time constant ( oneT ) = forty seven seconds, (from above). Therefore, fiveT = 5 x forty seven = 235 secs

d) The voltage across the capacitance when a hundred seconds?

The voltage formula is given as Vc = V(1 – e-t/RC)

which equals: Vc = 5(1-e-100/47) RC = forty seven seconds from higher than, Therefore, Vc = 4.4 volts

We have seen that the charge on a capacitance is given by the expression: letter of the alphabet = CV which once a voltage is foremost applied to the plates of the capacitance it charges up at a rate determined by its time constant, τ.

In the next tutorial {we will|we'll|we area unit going to} examine the current-voltage relationship of a discharging capacitance and appearance at the curves related to it once the capacitors plates are shorted along.